Trong hình học, một hình bình hành là một tứ giác có hai cặp cạnh song song. Hình bình hành có nhiều tính chất quan trọng, trong đó có tính chất về trục đối xứng. Trục đối xứng là một đường thẳng chia một hình thành hai nửa hình bằng nhau, khi gấp hình theo đường thẳng đó thì hai nửa hình sẽ chồng khít lên nhau.
Trong bài viết này, cùng Huanluyenantoanlaodong tìm hiểu về trục đối xứng của hình bình hành và các ứng dụng của nó trong giải toán.
Trục đối xứng của hình bình hành bình thường
Hình bình hành bình thường là một tứ giác có hai cặp cạnh song song nhưng không phải là hình chữ nhật hay hình vuông. Hình bình hành bình thường không có trục đối xứng vì nếu ta vẽ một đường thẳng cắt qua hình bình hành bất kỳ thì sẽ không có phần đối xứng so với phía còn lại của hình
Ví dụ: Hình dưới đây là một hình bình hành bình thường. Ta có thể thấy rằng không có đường thẳng nào chia hình này thành hai nửa hình giống nhau.
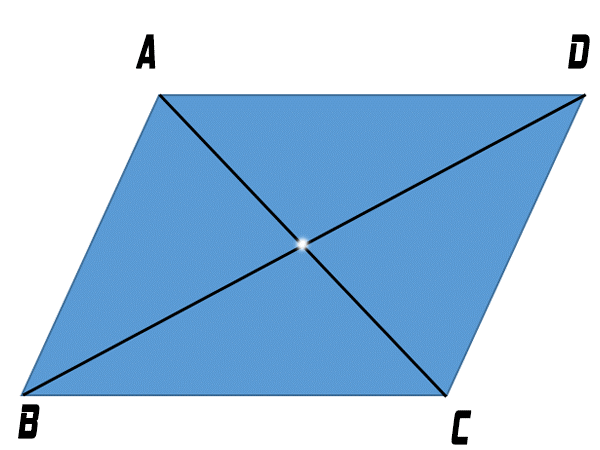
Trục đối xứng của các loại hình bình hành đặc biệt
Một số loại hình bình hành đặc biệt có trục đối xứng là:
- Hình chữ nhật: là một tứ giác có hai cặp cạnh song song và các góc vuông. Hình chữ nhật có hai trục đối xứng là các đường chéo của nó
Ví dụ: Hình dưới đây là một hình chữ nhật. Ta có thể thấy rằng các đường chéo AC và BD là các trục đối xứng của nó.
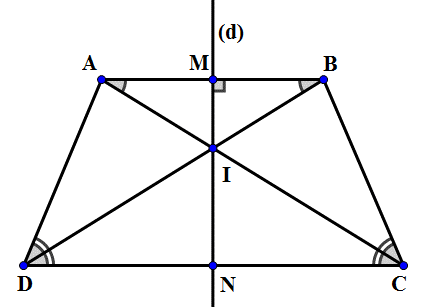
- Hình vuông: là một tứ giác có hai cặp cạnh song song, các góc vuông và các cạnh bằng nhau. Hình vuông có bốn trục đối xứng là các đường chéo và các trung trực của các cạnh
- Hình thoi: là một tứ giác có hai cặp cạnh song song và các cạnh bằng nhau. Hình thoi có hai trục đối xứng là các đường chéo của nó
Ví dụ: Hình dưới đây là một hình thoi. Ta có thể thấy rằng các đường chéo AC và BD là các trục đối xứng của nó.
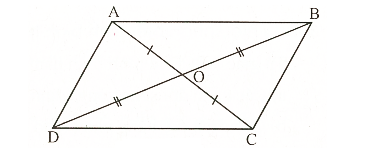
Ứng dụng của trục đối xứng trong giải toán
Trục đối xứng của hình bình hành có thể giúp chúng ta giải quyết một số bài toán liên quan đến tính diện tích, chu vi, góc, độ dài cạnh hay tọa độ điểm của hình bình hành. Dưới đây là một số ví dụ minh họa:
- Bài toán 1: Cho hình chữ nhật ABCD có diện tích là 24 cm2. Biết rằng trung điểm của cạnh AB là E, trung điểm của cạnh BC là F. Tính diện tích của tam giác AEF.
Giải: Ta có thể nhận thấy rằng đường chéo AC là trục đối xứng của hình chữ nhật ABCD. Do đó, tam giác AEF và tam giác CEF là hai tam giác đối xứng nhau qua AC. Vậy, diện tích của tam giác AEF bằng diện tích của tam giác CEF. Gọi S là diện tích của tam giác AEF, ta có:
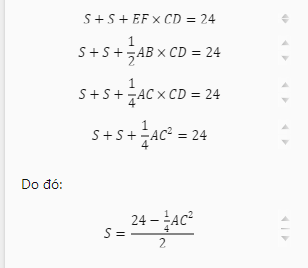
- Bài toán 2: Cho hình vuông ABCD có cạnh bằng 10 cm. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tính chu vi của tứ giác MNPQ.
Giải: Ta có thể nhận thấy rằng tứ giác MNPQ cũng là một hình vuông vì nó có các cạnh bằng nhau và các góc vuông. Để tính chu vi của tứ giác MNPQ, ta chỉ cần tính được độ dài cạnh MN. Ta có thể sử dụng trục đối xứng BD để suy ra rằng tam giác BMN và tam giác DQN là hai tam giác đối xứng nhau qua BD. Do đó, MN bằng DQ. Gọi x là độ dài cạnh MN, ta có:
- Bài toán 3: Cho hình thoi ABCD có đường chéo AC bằng 12 cm và đường chéo BD bằng 16 cm. Tính chu vi của hình thoi.
Giải: Ta có thể sử dụng trục đối xứng của hình thoi để giải bài toán này. Ta biết rằng các đường chéo AC và BD là các trục đối xứng của hình thoi, nên chúng chia hình thoi thành 4 tam giác vuông cân. Do đó, ta có thể áp dụng định lý Pythagoras để tính được độ dài cạnh AB của hình thoi. Gọi x là độ dài cạnh AB, ta có:
Các thiết kế hiện đại – hình thái biểu hiện của tính đối xứng trục
Các thiết kế hiện đại thực mang tư duy tổ hợp các bài toán đa trục, đáp ứng sự thay đổi thường xuyên và liên tục của môi trường sống. Tuy nhiên các không gian chính thông thường vẫn lưu giữ đặc tính có hướng làm cơ sở cho tạo dựng cấu trúc mang cả nội dung sử dụng và hình thức biểu hiện.
- Sân vận động Olympic Tokyo 2021
Thiết kế sử dụng các thành phần nhỏ kết nối với nhau tạo nên một cấu trúc lớn. Nó rất khác biệt với phương án giành giải Nhất của KTS Zaha Hadid bị cắt gọt, giảm mức đầu tư,… cuối cùng không được thực hiện.
Thiết kế được xây dựng là một hình mẫu điển hình đặc trưng của văn hóa mang cấu trúc đối xứng tương hỗ phương Đông mà cụ thể ở đây là Nhật Bản.
- Thư viện “Ngôi nhà Thông thái” tại Sharjah, UAE
Công trình thư viện sử dụng thiết kế đối xứng với mai đua và hệ chắn nắng truyền thống. Ý đồ thiết kế được hiện thực hóa bởi các công nghệ và vật liệu hiện đại, mái đua khẩu độ 15m và vật liệu nhôm nhưng với hình mẫu nan truyền thống.
“The House of Wisdom” tại Sharjah, UAE là một hình mẫu thư viện thế kỷ 21 đã chọn cấu trúc đối xứng làm hạt nhân đầu tiên.
- Bảo tàng Grand Egyptian Museum (GEM), Ai cập
Trong khu vực Giza của Ai cập với hàng loạt kim tự tháp, khó lòng tìm được một cấu trúc không đối xứng, tuy nhiên công trình xây mới hoành tráng và tham vọng nhất của Ai cập chính là ngoại lệ đó. Thông thường thì các bố cục đối xứng cho vật phẩm trưng bày là điều phổ biến nhất, tuy nhiên với bảo tàng có vô vàn vật phẩm như tại Cairo Ai cập thì cảm giác lộn xộn cũng không thể tránh khỏi.
Trong bài viết này, chúng ta đã tìm hiểu về trục đối xứng của hình bình hành và các ứng dụng của nó trong giải toán. Huanluyenantoanlaodong hi vọng bài viết này hữu ích với bạn!
