Trong bài viết này, Huanluyenantoanlaodong sẽ giới thiệu về một số công thức tính tổng các số hạng của một số dãy số đặc biệt, cũng như một số phương pháp và kiến thức liên quan để tính tổng các số hạng của các dãy số khác.
Giới thiệu về Công Thức Tính Tổng Các Số Hạng
Trong toán học, một dãy số là một chuỗi các số được sắp xếp theo một quy luật nào đó. Ví dụ, dãy số 1, 2, 3, 4, … là một dãy số có quy luật là mỗi số hạng bằng số hạng trước đó cộng với 1. Một dãy số có thể có số hạng hữu hạn hoặc vô hạn. Tổng các số hạng của một dãy số là giá trị thu được khi cộng tất cả các số hạng của dãy số đó lại với nhau. Ví dụ, tổng các số hạng của dãy số 1, 2, 3, 4 là 10.
Tính tổng các số hạng của một dãy số là một bài toán quan trọng và thường gặp trong toán học. Tuy nhiên, không phải mọi dãy số đều có công thức tính tổng các số hạng đơn giản và chính xác. Một số dãy số có công thức tính tổng các số hạng rất phức tạp hoặc không tồn tại. Do đó, cần có những phương pháp và kiến thức liên quan để giải quyết bài toán này một cách hiệu quả và chính xác.
Công thức tính tổng các số hạng của một số dãy số đặc biệt
Tổng các số hạng của một cấp số cộng
Một cấp số cộng là một dãy số có quy luật là mỗi số hạng bằng số hạng trước đó cộng với một hằng số gọi là công sai d. Ví dụ, dãy số 2, 5, 8, 11, … là một cấp số cộng có công sai d = 3.
Công thức tính tổng n số hạng đầu tiên của một cấp số cộng có công sai d và số hạng đầu tiên là a là:
Sn = 2n(2a + (n−1)d)
Chứng minh: Gọi S_n là tổng n số hạng đầu tiên của cấp số cộng. Ta có:
Sn = a + (a + d) + (a + 2d) + … + (a + (n−1)d)
Nhân hai vế với 2, ta được:
2Sn = 2(a + (a + d) + (a + 2d) + … + (a + (n−1)d))
Đổi chỗ hai đầu mút của dãy trong ngoặc tròn, ta được:
2Sn = 2((a + (n−1)d) + (a + (n−2)d) + … + (a + d) + a)
Cộng hai biểu thức trên lại, ta được:
2Sn = 2(a + (a + (n−1)d)) + 2((a + d) + (a + (n−2)d)) + … + 2((a + (n−1)d) + a)
2Sn = 2n(a + (n−1)d)
Sn = 2n(2a + (n−1)d)
Ví dụ: Tính tổng 10 số hạng đầu tiên của cấp số cộng có số hạng đầu tiên là 2 và công sai là 3.
Áp dụng công thức trên, ta có:
S10 = 10/2(2×2 + (10−1)×3)
S10 = 5(4 + 27)
S10 = 155
Tổng các số hạng của một cấp số nhân
Một cấp số nhân là một dãy số có quy luật là mỗi số hạng bằng số hạng trước đó nhân với một hằng số gọi là công bội q. Ví dụ, dãy số 2, 6, 18, 54, … là một cấp số nhân có công bội q = 3.
Công thức tính tổng n số hạng đầu tiên của một cấp số nhân có công bội q và số hạng đầu tiên là a là:
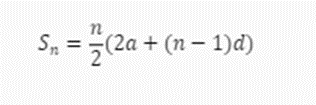
Công thức tính tổng dãy số cách đều
Công thức tính tổng dãy số cách đều = (số hạng đầu + số hạng cuối) x số số hạng có trong dãy : 2
Tính số cuối cách đều = số hạng đầu + (số số hạng – 1) x đơn vị khoảng cách
Tính số đầu cách đều = số hạng cuối– (số số hạng trong dãy – 1) x đơn vị khoảng cách
Tính số số hạng trong dãy = (số hạng cuối – số hạng đầu) : đơn vị khoảng cách + 1
Tính trung bình cộng = trung bình cộng của số hạng đầu và số hạng cuối trong dãy
Chú ý:
- Bài toán tính tổng dãy số cách đều thì ta chỉ nên quan tâm đến số hạng đầu, số hạng cuối và số số hạng có trong dãy, hai số liên tiếp cách nhau bao nhiêu đơn vị (đơn vị khoảng cách)
- TRong bài toán có số hạng là lẻ thì số ở giữa bằng ½ tổng mỗi cặp (số đầu + số cuối)
- Tùy vào bài toán tính dãy số tăng hoặc giảm để vận dụng vào những công thức trên sao cho phù hợp nhé
Ví dụ: Cho dãy số 2, 5, 8, 11, 14, 17, 20, 23, 26. Biết dãy số cách đều nhau 3 đơn vị, có 9 số hạng, số hạng đầu là 2 và số hạng cuối bằng 26
Lời giải:
Áp dụng công thức tính tổng dãy số cách đều ở trên ta có:
Tổng = (2 + 26) x 9 : 2 = 126
Số cuối = 2 + 3 x (9 – 1) = 26
Số đầu = 26 – 3 x (9 – 1) = 0
Số số hạng = (26 – 1) : 3 + 1 = 9,3
TB cộng = (2 + 5 + 8 + 11 + 14 + 17 + 20 + 23 + 26) : 9 = ( 2 + 26) : 2 = 14 hay = số ở giữa là 14
Một số bài toán về tính tổng dãy số cách đều và không cách đều
Bài tập 1: Tính giá trị của T biết: T = 2 + 3 + 4 + 5 +….+ 2015
Lời giải
Dãy số trên có số số hạng là: (2015 – 1) : 2 + 1 = 1008
Giá trị của T là: (2015 + 2) x 1008 : 2 = 1016568
Đáp số: 1016568
Bài tập 2: Tính tổng 40 số lẻ liên tiếp biết số lẻ lớn nhất trong dãy số là 2011?
Lời giải
Số hạng bé nhất trong dãy số đó là: 2011 – (40 – 1) x 2 =1933
Tổng của 40 số lẻ cần tìm là: (2011 + 1933) x 40 : 2 = 78880
Đáp số: 78880
Bài tập 3: Một khu phố có 25 nhà. Số nhà cuả 25 nhà đó được đánh là các số lẻ liên tiếp, biết tổng của 25 số nhà của dãy số đó bằng 1145. Hãy cho biết số nhà đầu tiên của khu phố đó là số bao nhiêu?
Lời giải
Hiệu giữa số nhà cuối và số nhà đầu tiên là: (25 – 1) x 2 = 48
Tổng của số nhà cuối và số nhà đầu là: 1145 x 2 : 25 = 91,6
Số nhà đầu tiên trong khu phố đó là: (91,6 – 48) : 2 = 21,8
Đáp số: 21,8
Huanluyenantoanlaodong hy vọng bài viết này sẽ giúp bạn có thêm kiến thức và kỹ năng để giải quyết bài toán tính tổng các số hạng của một dãy số.
