Trong bài viết dưới đây, Huấn luyện an toàn lao động sẽ cung cấp cho bạn đọc những thông tin liên quan đến Tính Chất 2 Mặt Phẳng Vuông Góc. Mời bạn đọc cùng theo dõi!
Giới thiệu về mặt phẳng trong hình học không gian -Tính Chất 2 Mặt Phẳng Vuông Góc
Trong hình học không gian, một trong những khái niệm quan trọng là mặt phẳng. Mặt phẳng là tập hợp các điểm trong không gian sao cho nếu lấy hai điểm bất kỳ trong tập hợp đó, đoạn thẳng nối hai điểm đó cũng thuộc tập hợp đó. Mặt phẳng có thể được xác định bằng nhiều cách, ví dụ như bằng ba điểm không thẳng hàng, bằng một đường thẳng và một điểm không thuộc đường thẳng đó, hoặc bằng hai đường thẳng song song.
Hai mặt phẳng được gọi là vuông góc nếu có một đường thẳng thuộc cả hai mặt phẳng và vuông góc với mỗi mặt phẳng. Ví dụ, trong hình lập phương, các mặt phẳng (ABC) và (ADH) là vuông góc với nhau, và đường thẳng AD là đường thẳng vuông góc chung của hai mặt phẳng này.
Tính Chất 2 Mặt Phẳng Vuông Góc
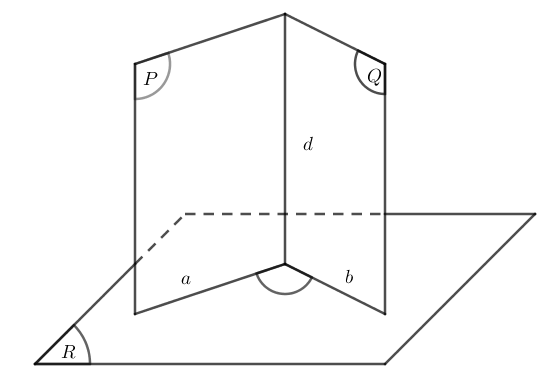
Từ khái niệm 2 mặt phẳng vuông góc, ta có thể suy ra một số tính chất sau:
- Nếu hai mặt phẳng vuông góc với cùng một mặt phẳng thứ ba, thì hai mặt phẳng đó song song với nhau. Điều ngược lại cũng đúng, tức là nếu hai mặt phẳng song song với nhau và vuông góc với một mặt phẳng thứ ba, thì hai mặt phẳng đó cũng vuông góc với nhau. Ví dụ, trong hình lập phương, các mặt phẳng (ABC) và (EFG) là song song và vuông góc với mặt phẳng (ADH).
- Nếu hai mặt phẳng vuông góc với nhau, thì các đường thẳng thuộc hai mặt phẳng đó cũng vuông góc với nhau nếu chúng cắt nhau. Ví dụ, trong hình lập phương, các đường thẳng AB và AD thuộc hai mặt phẳng (ABC) và (ADH) vuông góc với nhau và cắt nhau tại A.
- Nếu hai mặt phẳng vuông góc với nhau, thì các góc giữa các đường thẳng thuộc hai mặt phẳng đó có tổng bằng 90°. Ví dụ, trong hình lập phương, các góc giữa các cạnh AB và AE, hoặc giữa các cạnh AD và AH có tổng bằng 90°.
- Nếu hai mặt phẳng vuông góc với nhau, thì khoảng cách từ một điểm thuộc một mặt phẳng đến mặt phẳng còn lại bằng độ dài đoạn thẳng vuông góc chung của hai mặt phẳng đó và đi qua điểm đó. Ví dụ, trong hình lập phương, khoảng cách từ điểm B đến mặt phẳng (ADH) bằng độ dài đoạn thẳng BD.
Tính chất 2 mặt phẳng vuông góc có ứng dụng trong lĩnh vực nào?
Tính chất 2 mặt phẳng vuông góc có ứng dụng trong nhiều lĩnh vực khác nhau, như kiến trúc, cơ khí, định vị địa lý, v.v. Dưới đây là một số ví dụ:
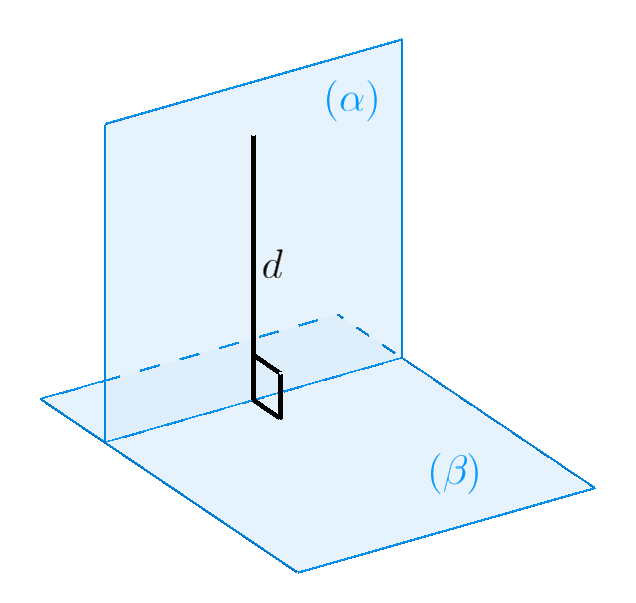
- Trong kiến trúc và xây dựng, tính chất 2 mặt phẳng vuông góc được sử dụng để thiết kế các kết cấu và công trình xây dựng có hình dạng chắc chắn, đẹp mắt và tiết kiệm không gian.
Ví dụ, các mặt phẳng của hình lập phương, hình hộp chữ nhật, hình chóp đều vuông góc với nhau, tạo ra các hình khối đơn giản và phổ biến trong kiến trúc
- Trong cơ khí và kỹ thuật, tính chất 2 mặt phẳng vuông góc được áp dụng để thiết kế các máy móc và hệ thống cơ khí có hiệu suất cao, độ chính xác cao và độ bền cao.
Ví dụ, các mặt phẳng của các bánh răng, các trục quay, các dao cắt, các bộ truyền động đều vuông góc với nhau, giúp cho việc truyền lực, cắt gọt, chuyển động được thuận lợi và ổn định
- Trong định vị địa lý, tính chất 2 mặt phẳng vuông góc được sử dụng để xác định vị trí của một điểm trên bề mặt trái đất hoặc trong không gian.
Ví dụ, các mặt phẳng của các tọa độ kinh tuyến và vĩ tuyến, hoặc của các tọa độ x-y-z đều vuông góc với nhau, giúp cho việc biểu diễn và tính toán khoảng cách, góc hướng, diện tích, thể tích được chính xác và tiện lợi
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về khái niệm và tính chất 2 mặt phẳng vuông góc. Đây là một nội dung cơ bản trong hình học không gian, có nhiều ứng dụng trong thực tế. Chúng ta có thể sử dụng các tính chất 2 mặt phẳng vuông góc để giải các bài toán liên quan đến hình lập phương, hình hộp chữ nhật, hình chóp, hình trụ, hình nón, hình cầu và các hình khác.
Huấn luyện an toàn lao động hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn về 2 mặt phẳng vuông góc và có thể áp dụng vào việc học tập và nghiên cứu.
