Trong bài viết này, hãy cung Huanluyenantoanlaodong tìm hiểu về các công thức tính thể tích lớp 12 của một số hình không gian phổ biến, cũng như các ví dụ minh họa và các ứng dụng thực tế của chúng.
thể tích là gì? Các Công Thức Tính Thể Tích Lớp 12
Thể tích là một đại lượng vật lý biểu thị khối lượng không gian mà một vật thể chiếm giữ. Thể tích có đơn vị là mét khối (m3) trong hệ đo lường quốc tế (SI). Trong hình học, thể tích của một hình không gian có thể được tính bằng nhiều cách khác nhau, tùy thuộc vào dạng và kích thước của hình đó.
Các Công Thức Tính Thể Tích Lớp 12
Thể tích của hình cầu
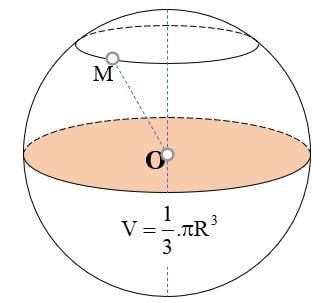
Hình cầu là một hình không gian có tất cả các điểm trên bề mặt cách một điểm cố định (gọi là tâm) bằng nhau. Bán kính của hình cầu là khoảng cách từ tâm đến bất kỳ điểm nào trên bề mặt. Công thức tính thể tích của hình cầu là:
V=4/3 πr3
Trong đó:
- V là thể tích của hình cầu.
- π là hằng số xấp xỉ bằng 3.14 hoặc 722.
- r là bán kính của hình cầu.
Ví dụ: Tính thể tích của một quả bóng có bán kính 15 cm.
Giải: Thay r=15 vào công thức, ta được:
V=34/3π(15)3≈14137.17 cm3
Thể tích của hình trụ
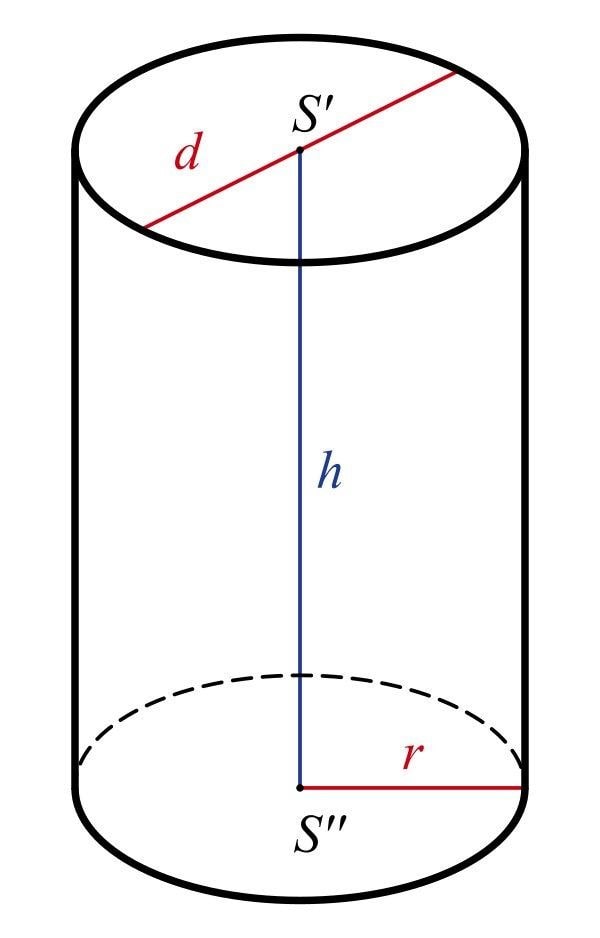
Hình trụ là một hình không gian có hai đáy song song và đồng dạng, và một mặt xung quanh nối hai đáy. Bán kính đáy của hình trụ là khoảng cách từ tâm đáy đến bất kỳ điểm nào trên đường tròn đáy. Chiều cao của hình trụ là khoảng cách giữa hai đáy. Công thức tính thể tích của hình trụ là:
V=π r2h
Trong đó:
- V là thể tích của hình trụ.
- π là hằng số xấp xỉ bằng 3.14 hoặc 722.
- r là bán kính đáy của hình trụ.
- h là chiều cao của hình trụ.
Ví dụ: Tính thể tích của một lon nước có bán kính đáy 3 cm và chiều cao 12 cm.
Giải: Thay r=3 và h=12 vào công thức, ta được:
V=π(3)2(12)≈339.29 cm3
Thể tích của hình nón
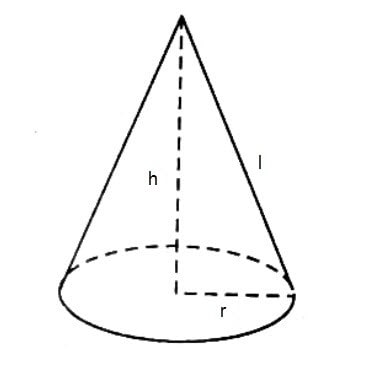
Hình nón là một hình không gian có một đáy là một đường tròn và một mặt xung quanh nối tâm đường tròn đáy với một điểm cố định (gọi là đỉnh). Bán kính đáy của hình nón là khoảng cách từ tâm đáy đến bất kỳ điểm nào trên đường tròn đáy. Chiều cao của hình nón là khoảng cách từ đỉnh đến mặt phẳng chứa đáy. Công thức tính thể tích của hình nón là:
V=1/3π r2h
Trong đó:
- V là thể tích của hình nón.
- π là hằng số xấp xỉ bằng 3.14 hoặc 722.
- r là bán kính đáy của hình nón.
- h là chiều cao của hình nón.
Ví dụ: Tính thể tích của một cái nón có bán kính đáy 5 cm và chiều cao 10 cm.
Giải: Thay r=5 và h=10 vào công thức, ta được:
V=1/3π(5)2(10)≈261.80 cm3
Thể tích của hình lập phương
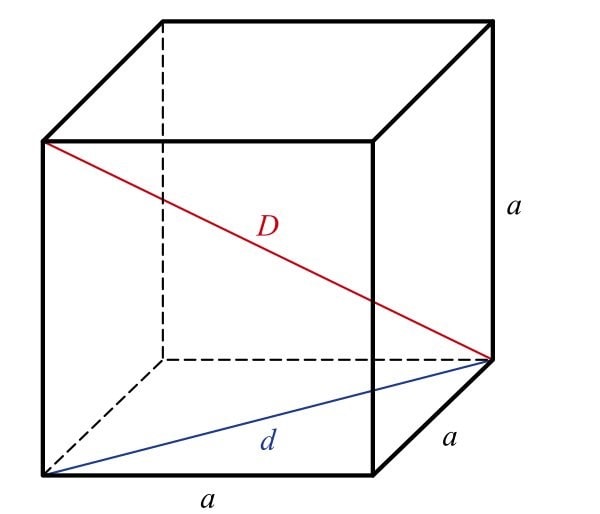
Hình lập phương là một hình không gian có sáu mặt là các hình vuông bằng nhau và song song theo từng cặp. Cạnh của hình lập phương là cạnh của một trong các hình vuông. Công thức tính thể tích của hình lập phương là:
V=a3
Trong đó:
- V là thể tích của hình lập phương.
- a là cạnh của hình lập phương.
Ví dụ: Tính thể tích của một khối Rubik có cạnh 3 cm.
Giải: Thay a=3 vào công thức, ta được:
V=(3)3=27 cm3
Thể tích của hình chóp
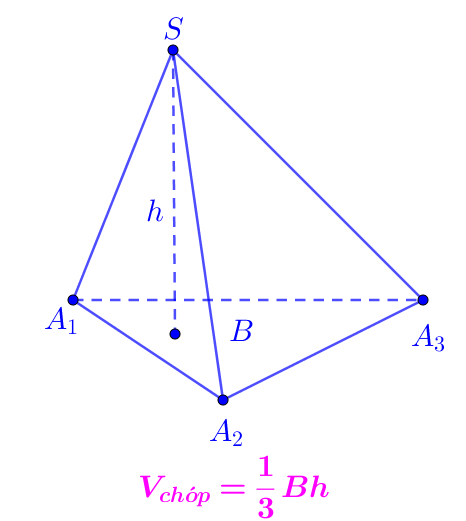
Hình chóp là một hình không gian có một đáy là một đa giác và các mặt xung quanh là các tam giác có chung một đỉnh (gọi là đỉnh chóp). Diện tích đáy của hình chóp là diện tích của đa giác đáy. Chiều cao của hình chóp là khoảng cách từ đỉnh chóp đến mặt phẳng chứa đáy. Công thức tính thể tích của hình chóp là:
V= (1/3)xSh
Trong đó:
- V là thể tích của hình chóp.
- S là diện tích đáy của hình chóp.
- h là chiều cao của hình chóp.
Ví dụ: Tính thể tích của một kim tự tháp có đáy là một hình vuông cạnh 20 m và chiều cao 30 m.
Giải: Thay S=202=400 m2 và h=30 vào công thức, ta được:
V=1/3 x [(400)(30)]=4000 m3
Trên đây là các thông tin liên quan đếnCác Công Thức Tính Thể Tích Lớp 12 mà Huanluyenantoanlaodong tổng hợp được. Hi vọng bài viết này hữu ích với bạn












![[GIẢI ĐÁP] Ma Túy Ketamin Là Gì Và Những…](https://huanluyenantoanlaodong.edu.vn/wp-content/uploads/2023/10/ma-tuy-ketamin-la-gi.html-2.jpg)
![[TÌM HIỂU] Niềng Răng Nên Kiêng Gì Và Những…](https://huanluyenantoanlaodong.edu.vn/wp-content/uploads/2023/09/nieng-rang-nen-kieng-gi.html-3-min.jpg)
![[TÌM HIỂU] Việc Tồn Tại Của Toàn Cầu Hóa…](https://huanluyenantoanlaodong.edu.vn/wp-content/uploads/2023/08/viec-ton-tai-cua-toan-cau-hoa-la.html-3-min.jpg)
![[TÌM HIỂU] Xesi Được Dùng Làm Tế Bào Quang…](https://huanluyenantoanlaodong.edu.vn/wp-content/uploads/2023/08/xesi-duoc-dung-lam-te-bao-quang-dien-1-min.jpg)
![[GIẢI ĐÁP] Vecto Gia Tốc Của Chất Điểm Có…](https://huanluyenantoanlaodong.edu.vn/wp-content/uploads/2023/08/vecto-gia-toc-cua-chat-diem-co-html-5-min.png)